La fonction LET de MS Excel

À l’ère de la data et de la complexification des normes comptables, les professionnels du chiffre (comptables, auditeurs, contrôleurs de gestion) font face à un défi permanent. Comment produire des analyses fiables, rapidement, tout en garantissant la traçabilité des calculs ? C’est dans ce contexte que la fonction LET d’Excel s’impose comme une révolution.

En fait, bien plus qu’une simple fonction, elle incarne une méthodologie de travail. Son secret ? Transformer l’écriture des formules en un processus structuré et documenté. 

Comprendre la fonction LET

La fonction LET agit comme un architecte de formules. En effet, elle permet de décomposer un calcul complexe en étapes nommées et logiques. Pour ce faire, Excel permet de nommer l’expression. Puis, la fonction LET donne le résultat en utilisant le nom donné précédemment. Ceci constitue un point essentiel pour des professionnels soucieux de précision et d’auditabilité.

Aussi, la fonction LET permet ainsi de gagner du temps. Elle conduit aussi à la création de formules beaucoup plus lisibles, et donc, davantage compréhensibles. En effet, en tant qu’utilisateur, on n’a pas besoin de retenir le contenu de la référence d’une cellule spécifique. C’est en fait un nom qui est donné à un calcul ou à une valeur à l’intérieur d’une formule.

Mécanisme et syntaxe 

La fonction LET repose sur une structure simple mais puissante :

=LET(nom1, valeur1, nom2, valeur2, …, calcul_final) qui contient plusieurs arguments, à savoir : 

• Noms de variables : Étiquettes explicites (Revenus, TauxTVA, Seuil) remplaçant les références cellulaires opaques.
• Valeurs associées : Peuvent être des nombres, des plages de cellules, ou même des formules intermédiaires.
• Calcul final : Résultat utilisant les variables nommées, évitant les répétitions.

Ainsi, avec la fonction LET, il est possible d’avoir de nombreuses paires de noms et de valeurs. Autrement dit, à chaque nom correspond une valeur. Au total, la fonction LET contient 126 paires dans une même formule.

Maintenant, voyons un exemple élémentaire, celui du calcul d’une marge brute : 

=LET(  

            Ventes; B3;  
            Coûts; C3,  
            Marge_Brute ; Ventes – Coûts;  
           Marge_Brute  

) 

Ainsi, chaque étape est lisible comme une phrase : « Soient les Ventes, les Coûts, alors la MargeBrute est Ventes – Coûts ». On voit bien ici que le dernier argument de la fonction LET est le nom de la variable i.e. Marge_Brute auquel on souhaite afficher le résultat.

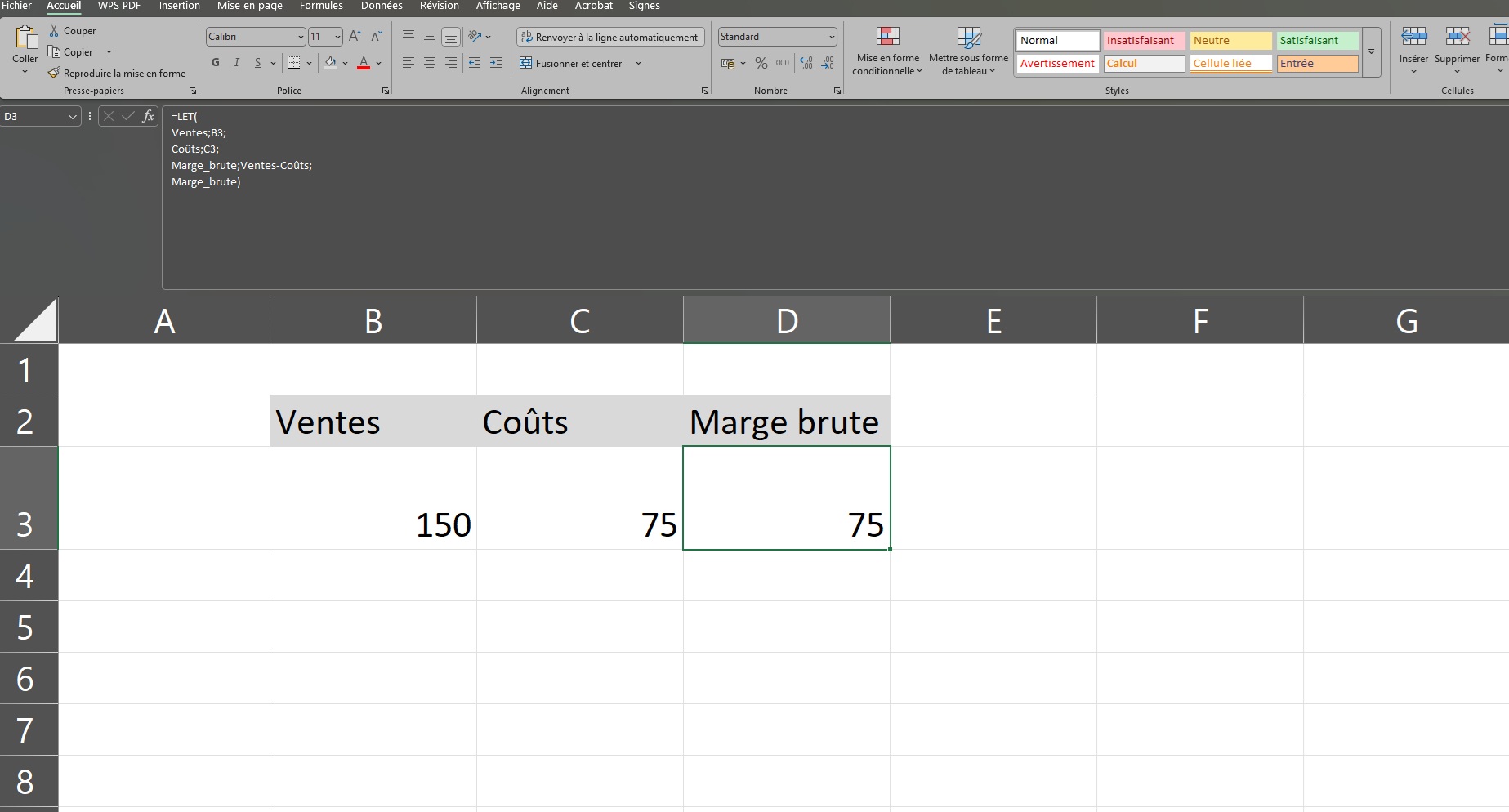
A noter que pour voir la formule de la fonction LET entièrement, il convient d’abaisser la barre de formule. En premier lieu, on y inscrit la fonction LET, à savoir =LET( . Puis, pour aller à la ligne, on appuie simultanément sur les touches de son clavier ALT+ENTREE.

Applications basiques en comptabilité

Ainsi, pour les métiers du chiffre, LET brille dans des scénarios récurrents :

D’abord, prenons l’exemple du calcul de TVA avec variables nommées :

=LET(  

           Montant_HT; B3;  
           TauxTVA; 20%; 
           TVA; Montant_HT * TauxTVA; 
           Montant_HT + TVA

) 

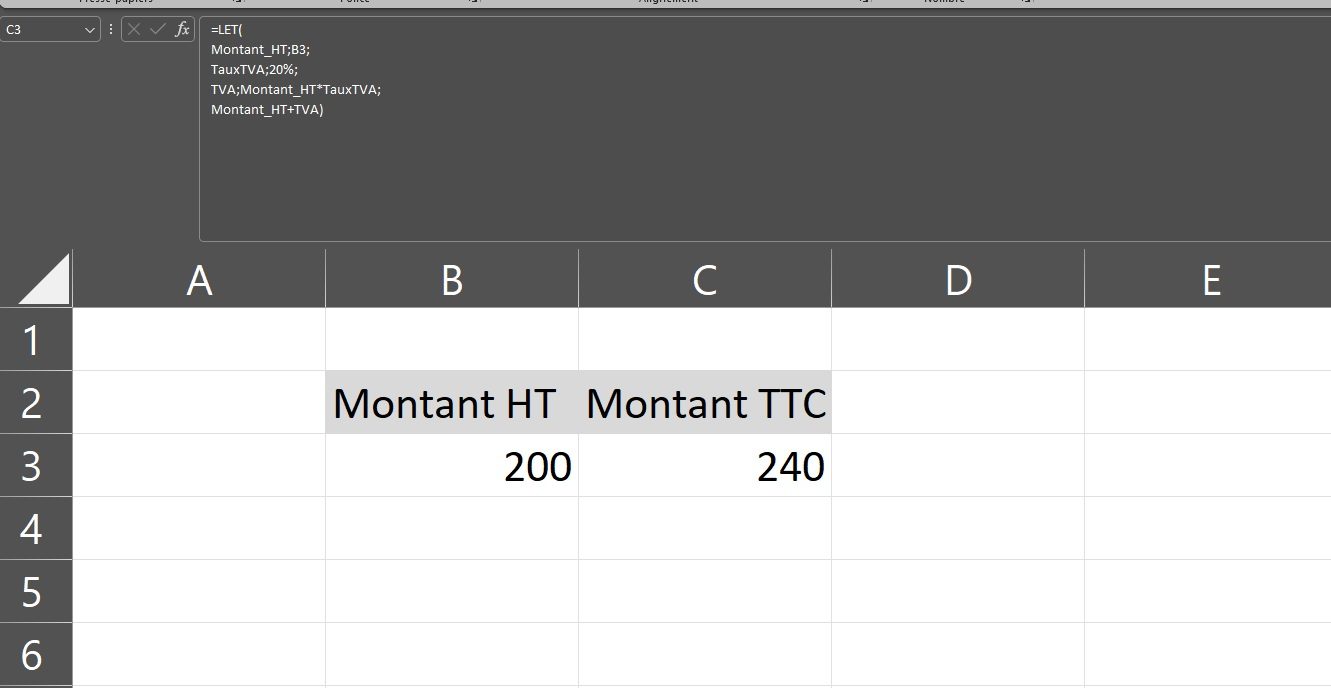Ainsi, l’intérêt de la fonction LET ici est de souligner le fait que le taux de TVA est centralisé. Par conséquent, un changement de législation (ex: 22%) ne nécessite qu’une modification.

Ensuite, voyons un autre exemple basique, celui des seuils d’audit réutilisables :

=LET(  

           Transaction; A3;  
           Seuil; 10000;  
          SI(Transaction > Seuil; « À vérifier »; « OK »)  

 )

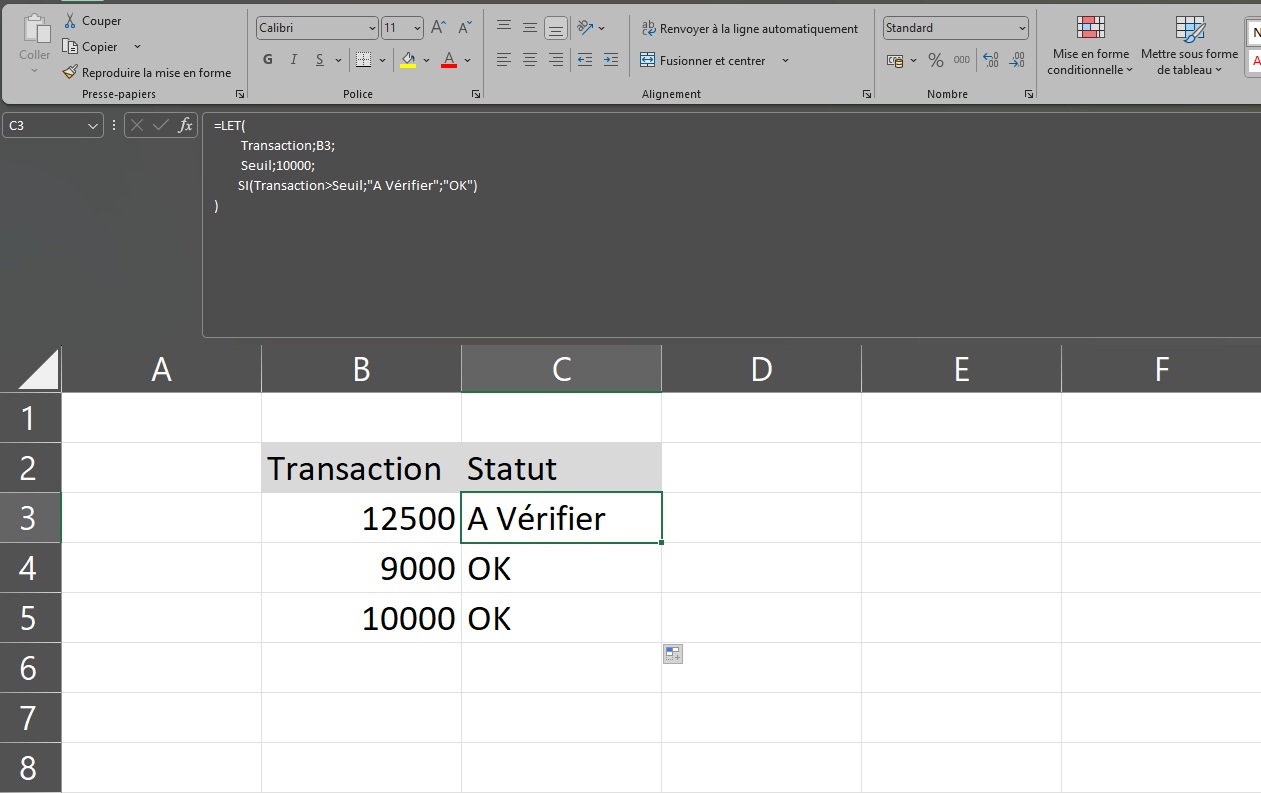
Ainsi, comme dans l’exemple précédent, le seuil de 10 000 € est défini une fois. L’avantage alors est d’éviter des répétitions risquées. En fait, la formule teste si la transaction dépasse le seuil. Dans la positive, elle affiche : « A vérifier », sinon, OK.

Maîtriser LET : Applications avancées et valeur ajoutée stratégique

La fonction LET n’est pas qu’un outil de productivité. Elle devient un levier de qualité pour les rapports financiers, les audits et la collaboration entre équipes. Ainsi, cette fonction conduit à formaliser des bonnes pratiques calculatoires.

Cas d’usage avancés de la fonction LET : Industrialisation des calculs sectoriels

Aussi, les professionnels expérimentés exploitent LET par exemple pour :

–d’une part, procéder à des calculs d’amortissements personnalisés avec variables explicites.
– d’autre part, faire l’analyse d’écarts budgétaires multicritères :

Calcul des amortissements

=LET(  

            CoûtActif ; B2;  
            ValeurRésiduelle ;  C2;  
            Durée; D2;  
            BaseAmortissable ; CoûtActif – ValeurRésiduelle;  
            AmortissementAnnuel ; BaseAmortissable / Durée; 
           AmortissementAnnuel  

         )

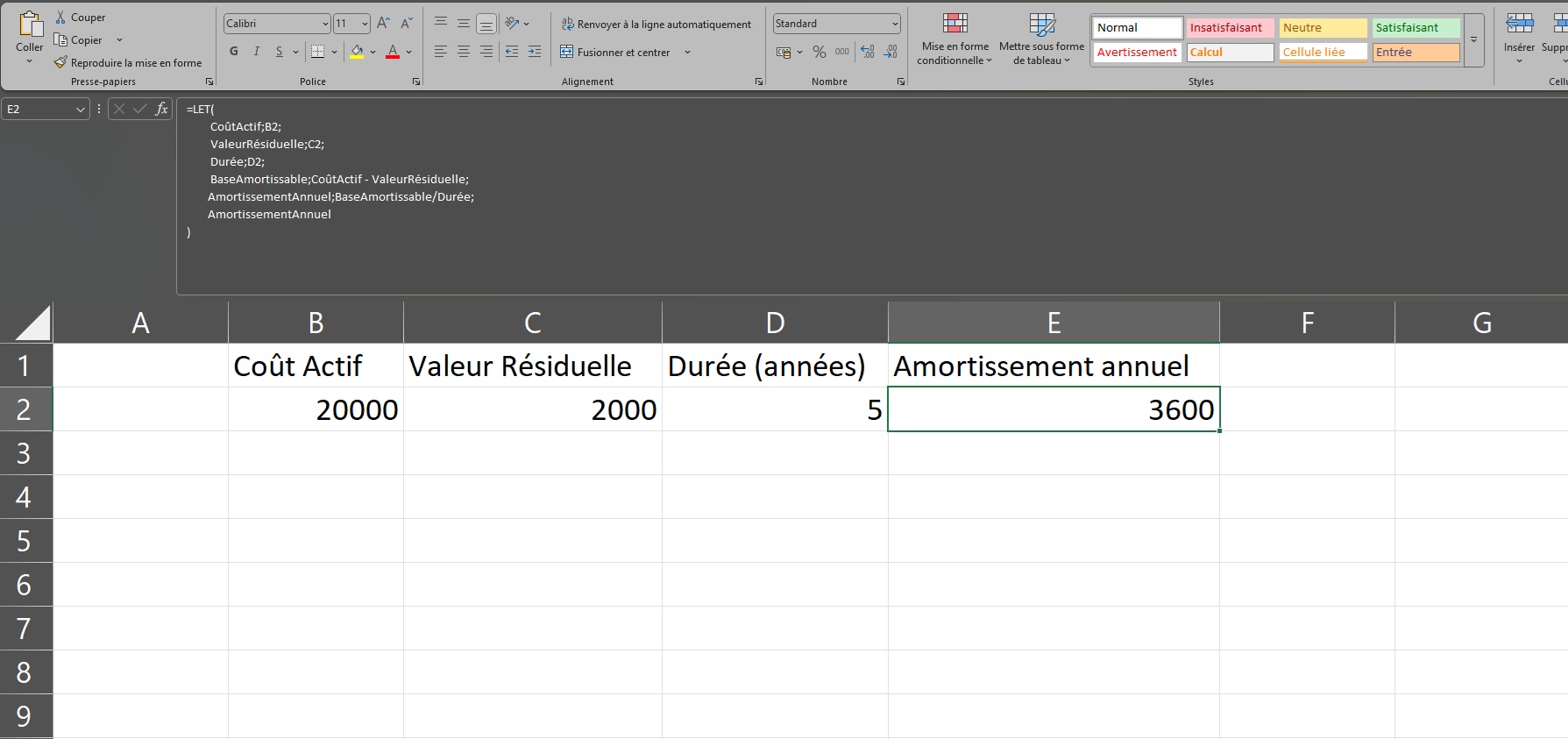
Ainsi, la fonction LET s’applique bien au calcul de l’amortissement annuel linéaire pour un actif donné. L‘avantage ici est de souligner la logique comptable (normes IAS/IFRS). En effet, en nommant chaque étape du calcul (coût d’acquisition, valeur résiduelle, base amortissable, durée, amortissement annuel), la fonction LET rend la formule transparente et conforme à la logique des normes comptables internationales. Or, celles-ci exigent de distinguer ces éléments dans le calcul de l’amortissement.

Plus précisément, les normes, y compris l’IFRS 16, imposent de calculer l’amortissement sur la base du coût d’acquisition diminué de la valeur résiduelle, réparti sur la durée d’utilité. C’est donc cette démarche que reflète la structure de la formule LET. 

En conséquence, celle-ci est visible et vérifiable par les auditeurs lors d’un audit ou d’un contrôle interne.

Calcul d’écarts budgétaires

=LET(  

           Budget; B2;  
           Réel; C2;  
           SeuilPourcent ;  10%;  
           SeuilMontant ;  5000;  
          Écart ;  Réel – Budget; 
          ÉcartAcceptable ; SI(ABS(Écart) > Budget * SeuilPourcent; « Non »; « Oui »); 
          SI(ET(ÉcartAcceptable = « Non »; ABS(Écart) > SeuilMontant); « Alerte majeure »; « Contrôle standard »)  

    )

 

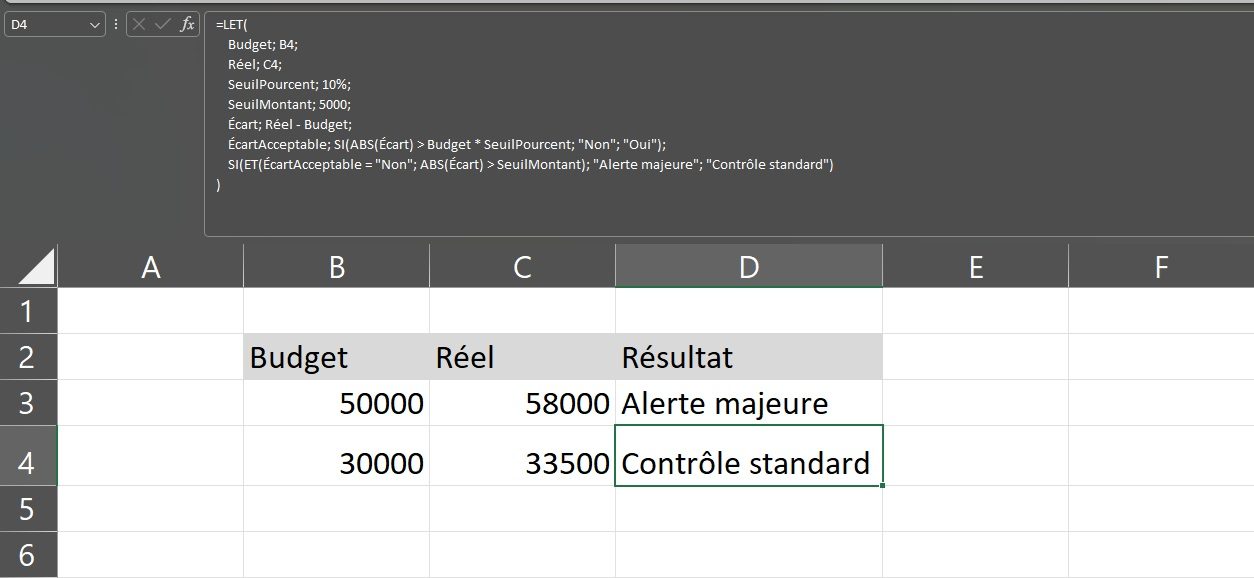
Concrètement, la fonction LET permet de poser les différentes étapes du calcul. Tout d’abord, on inscrit dans cette fonction les données dont on dispose : Budget en cellule B3 a pour valeur 50 000 et le réel en cellule C3 est de 58 000. Puis, on détermine un seuil relatif SeuilPourcent de 10% et un seuil absolu SeuilMontant de 5 000. Ensuite, on détermine un écart, soit la différence entre le réel et le budget i.e. 58 000-50 000=8 000. Enfin, on détermine l’écart acceptable, soit ABS(8000) > 50 000 *10% c’est-à-dire 8 000 >5000 qui aboutit à la réponse « NON ».

De plus, la dernière étape de la fonction LET vérifie que si EcartAcceptable = « Non » et ABS(8 000) > 5 000 est vrai, alors il s’agit d’une « alerte majeure ».

En revanche, dans le 2ème cas, avec un budget de 30000 et un réel de 33500, donc, pour un écart de 3500, on aboutit à un contrôle standard. En effet, le seuil relatif correspond à 30 000 * 10% = 3 000 → Écart (3500) > 3 000 , d’où la réponse « Non ». Or, comme une seule condition est remplie, le seuil absolu 3500<5000 aboutit à un contrôle standard.

Intérêt du modèle

Par conséquent, en combinant seuils relatifs (10%) et absolus (5000€), la fonction LET présente un gain significatif en termes de traçabilité. En effet, les variables SeuilPourcent et SeuilMontant sont nommés en début de formule. Cela permet à tout utilisateur (comptable, auditeur, direction) de comprendre immédiatement les règles appliquées sans avoir à décrypter des références de cellules ou des calculs imbriqués.

Qui plus est, la formule devient auto-explicative. Ceci constitue un élément crucial en audit ou en contrôle interne où la justification des seuils est souvent requise. Enfin, la logique métier est clairement respectée par les différentes étapes (détermination des seuils, calcul de l’écart et application de règles de contrôle).

Valeur ajoutée métier de la fonction LET : Auditabilité, collaboration et gain de temps

Si la fonction LET simplifie efficacement les calculs simples, son véritable potentiel se révèle dans la gestion de processus complexes. Elle s’impose ainsi comme un outil stratégique de gouvernance des données. En structurant les formules sous forme d’algorithmes documentés, elle permet aux professionnels de la finance de dépasser la dimension technique pour se concentrer sur l’analyse stratégique. Comme vu précédemment, cette approche favorise l’intégration de logiques métier sophistiquées, tout en renforçant la collaboration entre équipes.

Simplification des calculs complexes

Tout d’abord, la fonction LET permet de décomposer des processus métier complexes en étapes nommées et documentées.  Prenons l’exemple d’un calcul de provision pour créances douteuses en audit : elle permet d’intégrer des variables telles que seuil_risque, historique_impayés ou ratio_couverture dans une formule claire.

=LET(  

historique_impayés; MOYENNE(D2:D100);  
seuil_risque; 0,05;  
ratio_couverture; 1,2; 
provision; historique_impayés * ratio_couverture * seuil_risque;  
provision  

) 

Aussi, cette modularité rend la logique métier immédiatement compréhensible et adaptables aux évolutions réglementaires ou stratégiques.

De plus, en attribuant un nom à chaque variable, LET transforme une formule technique en un processus documenté. En fait, cette fonctionnalité répond à trois enjeux majeurs en contrôle financier :

En premier lieu, grâce à la transparence, les formules auto-explicatives facilitent les revues par les pairs et les vérifications externes. Ensuite, l’auditabilité permet aux auditeurs de retracer chaque étape d’un calcul sans décrypter des formules imbriquées. Enfin, la centralisation de variables communes comme, par exemple, seuil_matérialité garantit la cohérence des modèles financiers. 

Du technique au stratégique : un changement de paradigme

Enfin, en réduisant la complexité opérationnelle, LET permet de se consacrer à des missions à plus haute valeur ajoutée :

En effet, d’une part, les auditeurs se consacrent davantage à l’interprétation des risques. Mais aussi, il est possible de modifier les paramètres stratégiques sans risques d’erreur. De plus, dans une logique collaborative, ces formules standardisées servent de langage commun entre équipes techniques et décisionnelles (ex. direction financière).

Par exemple, en guise d’illustration pratique en audit, considérons un test de matérialité sur des écritures comptables :

=LET(  

ecriture; A2;  
seuil_materialité; 10_000;  
ecriture_abs; ABS(ecriture); 
SI(ecriture_abs > seuil_materialité ; « Contrôle approfondi »; « Accepté »)  

) 

Par conséquent, cette implémentation permet à un non-technicien de comprendre instantanément la logique de contrôle. Qui plus est, elle permet aussi une adaptation rapide du seuil de matérialité selon le contexte réglementaire.

Toutefois, si LET est un outil puissant, il s’inscrit dans une démarche plus large de gouvernance data (normes de modélisation, documentation externe, etc.). Son vrai potentiel émerge quand il est couplé à des bonnes pratiques de conception de fichiers (naming des variables, commentaires, etc.).

Conclusion

En conséquence, la fonction LET transcende la simple optimisation technique. En fait, elle incarne une nouvelle philosophie d’utilisation d’Excel pour les professionnels du chiffre. Ainsi, en structurant les formules comme des enchaînements logiques documentés, elle répond à trois impératifs clés du secteur :

Premièrement, cette fonction élimine des erreurs de répétition et des incohérences grâce à la précision. De plus, elle fait preuve de transparence puisque les formules peuvent être auditées en quelques secondes. Enfin, la fonction LET est extrêmement agile. Elle a ainsi cette capacité à modifier des paramètres globaux (taux, seuils) en temps réel.

Ainsi, dans un environnement où la donnée constitue une ressource stratégique majeure, la maîtrise de LET représente un véritable levier de performance. Elle s’impose dès lors comme une compétence essentielle à maîtriser pour tout professionnel du chiffre.

Pour aller plus loin :